TS EAMCET 2017 :: Physics :: General questions

• Physics - General questions

A thermocol box has a total wall area (including the lid)  of 1.0 m² and wall thickness of 3 cm. It is filled with ice at $0^{0}C$. If the average temperature outside the box is $30^{0}C$ throughout  the day, the amount of ice that melts in one day is 

[Use $K_{termocol}= 0.03 W/mK,$

  $L_{fusion(ice)}=300 \times 10^{5} J/kg$]

Answer:

Explanation:

 Given,

 Total wall area (including the lid) (A)=1.0 cm²

 Thickness of wall(l)=3 cm= $3 \times 10^{-2} m$

 Average temperature outside  the box = $30^{0}C$

 $\triangle \theta =30-0= 30^{0}C$

 $L_{fusion (ice)}=3 \times 10^{5} J/kg$

 $K_{thermocol}=0.03 W/m K$

 We know that,

    $\frac{Q}{t}=\frac{KA}{l} \triangle Q$

 For one day, t=24 x 60 x 60 s

$\frac{ m \times L_{fusion (ice)}}{t}=\frac{KA}{l} \triangle Q$

  $\frac{m\times3\times 10^{5}}{24\times60\times60}=\frac{0.03\times1}{3\times 10^{-2}}\times30$

   $m=\frac{0.03\times1 \times30\times24\times 60\times60}{3\times 10^{-2}\times3\times10^{5}}$

   $m= \frac{77760}{9000}$= 8.64 kg

A parallel beam of light of intensity $I_{0}$ is incident on a coated glass plate. If 25% of the incident light is reflected from the upper surface and 50% of light is reflected from the lower surface of the glass  plate, the ratio of maximum to minimum  intensity  in the interference region of the reflected light is 

Answer:

Explanation:

 According to question , we can draw the following  diagram

  $I_{1}=\frac{I_{0}}{4} \Rightarrow  I_{2}= \frac{3}{8} I_{0}$

 We know that,

 $\frac{ I_{max}}{I_{min}}$= $\frac{(\sqrt{I_{1}}+\sqrt{I_{2}})^{2}}{(\sqrt{I_{1}}-\sqrt{I_{2}})^{2}}=\left(\frac{\frac{1}{2}+\sqrt{\frac{3}{8}}}{\frac{1}{2}-\sqrt{\frac{3}{8}}}\right)^{2}$

Consider a solenoid carrying current supplied by a DC  source with a constant emf containing iron core inside it. When the core is pulled out of the solenoid, the change in current will 

Answer:

Explanation:

When the core is pulled out  the solenoid, the change in current will remain the same

 A meter scale made of steel , reads accurately at $25^{0}$ C.  Suppose  in an experiment an accuracy of 0.06 mm in 1 m is required, the range of temperature in which the experiment can be performed with this meter scale  is (coefficient of linear expansion of steel is $11 \times 10^{-6} /° C)$

Answer:

Explanation:

 Given , coefficient of linear  expansion  of steel,

  $\alpha = 11 \times 10^{-6}  / ^{0} C$

 We know that,

 $\triangle l= l \alpha \triangle t \Rightarrow \triangle t = \frac{ \triangle l}{ l \alpha}$

 Here, $\triangle l= 6 \times 10^{-5} m \Rightarrow l=1m$

 $\triangle t= \frac{ 6 \times 10^{-5}}{1 \times 11 \times 10^{-6}}$

              =$5.45^{0} C$

 So, the range of temperature in which the experiment  can be hence performed him this  metre scale will be $19^{0}C to 31^{0}C$

 Here, option (a) is correct

A wooden box lying at rest on an inclined surface of wet wood is held at static equilibrium by a constant force F applied perpendicular to the incline. If the mass of the box  is 1 kg , the angle of inclination is $30^{0}$  and the coefficient of static  friction between the box and the inclined plane is 0.2, the minimum magnitude of F is (Use g=10 m/s ² )

Answer:

Explanation:

 According to question , we can draw the following  diagram

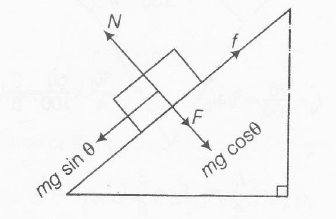
 $mg \sin \theta= \mu (F+ mg \cos \theta)$

 $F= \frac{mg \sin \theta}{\mu}-mg \cos \theta$

 $F=mg\left[\frac{\sin \theta}{\mu}-\cos \theta\right]$

 Here,

     m=1kg ,g=10 m/s², $\theta=30^{0}$, $\mu=0.2$

 $F=1\times 10\left[\frac{\sin 30}{0.2}-\cos 30^{0}\right]$

     = $10\left[\frac{1}{2\times 0.2}-\frac{\sqrt{3}}{2}\right]$

  = $10\left[\frac{5}{2}-\frac{\sqrt{3}}{2}\right]=5[5-\sqrt{3}]$

   =$5[5-1.732]=16.34 N$

• Physics - General questions